| Les techniques de résolution > 3- Les ensembles
3.1 Ensembles nus
- 3.1.1 paire nue
Quand un groupe contient deux cases avec une même paire de candidats (et eux seuls) alors ces candidats ne peuvent se trouver dans une autre case du groupe. Cela fonctionne pour une ligne, une colonne ou un carré.
 |
Sur la 2ème ligne, on a la paire 1,4 en G2 et H2. On peut en déduire que si 1 est en G2, alors 4 est en H2 ou vice et versa. Mais ces deux cases contiendront forcément 1 et 4. On peut donc les supprimer du reste de la ligne.
Comme ces paires appartiennent toutes les deux au 3ème carré à droite), alors on peut aussi éliminer 1 et 4 des autres cases de ce carré.
|
|
|
- 3.1.2 Triplet et quatrain
Quand trois cases d'un groupe ne contiennent pas d'autres chiffres que trois candidats, ces chiffres peuvent être exclus des autres cases du groupe. Attention! Il n'y a pas besoin que ces trois cases contiennent tous les chiffres du triplet, il faut seulement que ces cases soient les seules à avoir les trois chiffres en commun.
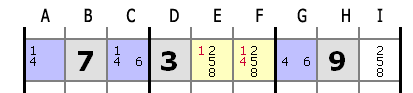 |
Sur cette ligne, on a dans les cases A, C et G le triplet 1,4,6 ou deux candidats de ce triplet. Ces trois cases vont forcément contenir les trois chiffres de ce triplet, ils ne peuvent donc être ailleurs sur la ligne.
On peut les supprimer des autres cases (ici E et F) avec certitude.
|
|
|
- De même pour un quatrain, si quatre cases ne contiennent pas d'autre candidats qu'un quatrain déterminé, alors ces chiffres peuvent être exclus des autres cases du groupe. Comme pour le triplet, les cases contenant le quatrain n'ont pas à contenir les quatre chiffres du quatrain.
Plus généralement, pour un nombre N de candidats d'un groupe, il faut trouver N cases qui contiennent ces candidats. Chaque case doit contenir un des candidat, donc pour trois cases contenant un triplet (même incomplet), les trois chiffres du triplet vont être répartis sur ces trois cases, et ne pourront donc pas être dans une autre case du groupe.
3.2 Ensembles cachés
Pour les ensembles nus (voir 3.1), les paires, triplets et quatrains permettent de supprimer des candidats dans le reste du groupe. Avec cette technique, les paires, triplets et quatrains permettent de supprimer les autres candidats des cases les contenant.
S'il y a N cases (2,3 ou 4) contenant N chiffres en commun, alors tous les autres candidats de ces cases peuvent être exclus.
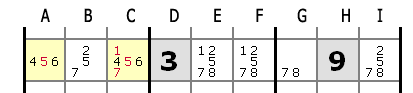 |
Sur cette ligne, la paire 4,6 ne se trouve que dans les cases A et C.
On peut donc éliminer les autres candidats pour ces deux cases car elles contiendront forcément soit 4, soit 6 et rien d'autre.
|
|
|
Comme pour les triplets et quatrains nus (3.1.2), les cases n'ont pas besoin de contenir tous les chiffres du triplet/quatrain. Les triplets cachés sont très difficiles à repérer, ils sont heureusement rarement utiles pour résoudre un sudoku. Les quatrains ne peuvent pratiquement pas être décelés!
|
|




